Advice for borderline AIME qualifiers

At this point you should be able to solve problems and self-study. When starting out, the most important thing to do is to get your feet wet and not think too much about strategy, pedagogy, etc. Right now the reverse is true. You can’t get good at math just by knowing things anymore. Now you have to sort things out in your head.

In the test

The two main things that newer contestants struggle with are making stupid mistakes (“sillying”) and speed. Neither of these can really be improved by mindless grinding. Plus, you do not need to be very fast to get a good score — unless you are literally aiming for a perfect score, for most people getting around 130 on the AMCs is enough.

The main way to solve AMC problems fast enough and accurately is to think about them as simply and as clearly as possible. Introduce as few things — whether these are variables or steps — as you can, and though you should not actually be writing every step on the test, make sure you explicitly know what they are in your head. Do this as you are doing each problem, and if time permits (which it should, although the last few years have been a crapshoot), do this immediately after again.

It’s rare that you can or should brute force your way through an AMC problem. In recent years this has become less true, so this advice isn’t as strong as it would be before. But it still holds for at least 80% of all the problems.

Sort your brain

You should have a framework of everything you know in math contests. For instance, you should know the area formulae connect to each other as shown in the image below.

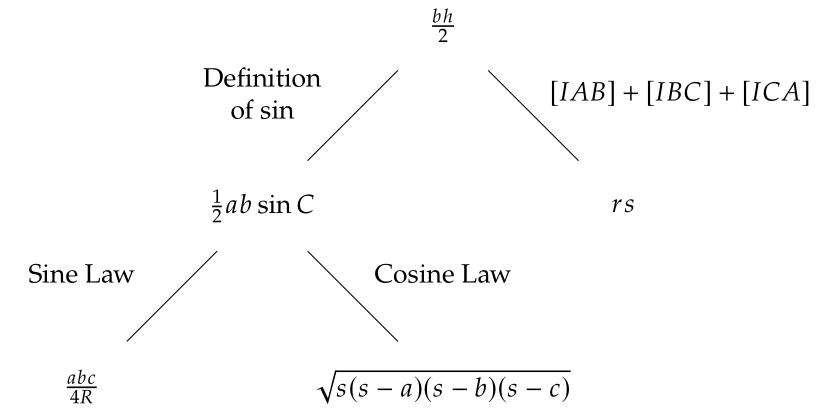
Chart of area formulae

The best way to do sort everything out in your head is to write. You can write handouts, notes, books, or whatever. Just write about what you’re learning in some way. Write outlines of the solutions to medium-hard AMC and AIME problems and keep track of them somewhere. It’s totally fine if what you write is complete garbage at first. I definitely did, and I can’t deny that seeing the material that I wrote two or three years ago is incredibly embarrassing.

The idea isn’t to practice speed. The idea is to sort out “What the heck is happening in my head?” Speed will come naturally with that. It’s like cleaning up your room. Of course you’ll find things faster with a neat room. The way to find things in your room faster isn’t to practice finding stuff in your room, or giving yourself a lower time limit to find things in your room. It’s to clean the darn thing, for crying out loud.

But there’s a difference between cleaning your room and sorting your brain. Your room gets dirtier the more you use it. Your brain gets cleaner and more efficient the more you use it. And the best way to use and sort your brain is to write. And you might end up giving back to the math community that gave you so much in the process, which is certainly a very pleasant byproduct.

Sort. Write. Polish. That’s really it.

Reach

The goal of preparing for math contests is to alter your model of how to do problems so you can do more of them. You want to do this as efficiently as possible, which means you should try to learn as much from each problem you do as possible. (Contrary to popular belief, good problems are sort of limited. You won’t ever run out, but each new source of good problems does get harder to find.)

It does not make sense to spend your time grinding 1-15 if you already know how to do all of those problems. Your internal model is not really getting updated, and you are just wasting your time. This is why I anti-recommend grinding past tests, because 30 of those 75 minutes are wasted on 1-15. (Also, you can’t start doing a test in the middle of class, but you can pull out problems to do them in an untimed manner.) Nor should you be doing problems that you completely do not understand.

You should spend most of your time doing problems that are slightly above your level. Evan Chen has a good blog post on this.

The way to expand your reach is by noticing common trends, and the only way you can do that is by taking notes and looking at more than one problem at a time. Say you come across these three problems that require you to pair stuff up:

How many ways can

n

coins be flipped such that an even number of heads comes up?

Any series of flips with heads at the end can be paired with the exact same series of flips except with tails at the end. Since one of them has an even number of heads and the other has an odd number of heads, exactly half of all possible series of flips have an even number of heads.

Since there are $2^n$ possible series of flips, there are $2^{n-1}$ series of flips such that an even number of heads come up.

(AIME 1983/13) For

\{1, 2, 3, \ldots, n\}

and each of its non-empty subsets a unique alternating sum is defined as follows. Arrange the numbers in the subset in decreasing order and then, beginning with the largest, alternately add and subtract successive numbers. For example, the alternating sum for

\{1, 2, 3, 6, 9\}

9-6+3-2+1=5

and for

\{5\}

it is simply

5

. Find the sum of all such alternating sums for

n=7

Note that any subset

A

not containing

7

can be matched with a subset

B

containing

7

, and further note that

S(A)+S(B)=7

. Since there are

2^6=64

sets

A

(we can treat the empty set as having alternating sum

0

), the answer is

64\cdot 7=448

(Summer MAT 2021/9) Alexander is juggling balls. At the start, he has four balls in his left hand: a red ball, a blue ball, a yellow ball, and a green ball. Each second, he tosses a ball from one hand to the other. If Alexander juggles for

20

seconds and the number of ways for Alexander to toss the balls such that he has all four balls in his right hand at the end is

N

, find the number of positive divisors of

N

Let $L$ and $R$ denote the number of ways to finish with all of the balls in his left and right hand, respectively. Then the idea is trying to find $L+R$ and $L-R$ .

Note that $L+R$ is just the number of ways to end with all four balls in one hand.At the end of $18$ seconds, he either has $4$ balls all in the same hand or $2$ balls in each. Now notice that no matter what, at the $19$ th second, he will always have $3$ balls in one hand and $1$ in the other. Now at the last second, there is exactly one move that can get him to four balls in one hand, so $L+R=4^{19}$ .

Now we examine $L-R$ . Note that if Alexander ever has two balls in the same hand, then the number of ways to finish with all balls in the left hand is the same as finishing with the right hand by symmetry. Thus, the only situation that contributes to $L-R$ is when we continually alternate between $4$ balls in the left hand, none in the right and $3$ balls in the left hand, $1$ on the right! Note that to have all balls in the right hand, we must have $2$ balls in the right hand at some point, so we just need to count the number of ways to end with all $4$ balls in the left hand without two ever reaching the right hand at the same time. The total difference is just $L-R=4^{10}$ .

Now note that

R=\frac{(L+R)-(L-R)}{2}=\frac{2^{38}-2^{20}}{2}=2^{37}-2^{19}=2^{19}(2^{18}-1)

, and by factoring with difference of squares and sums/differences of cubes, we get that this is equivalent to

2^{19} \cdot 3^3 \cdot 7 \cdot 19 \cdot 73

Thus the answer is $20\cdot 4\cdot 2\cdot 2\cdot 2=640$ .

If you are not paying attention, or you only have the chance to look at each of these problems individually, you will just look at each of them and say “how clever”. Even if you solved all of these problems, you would be unlikely to know how to prove PIE. But if you have sufficiently good intuition and you took notes on all three of these problems, particularly AIME 1983/13, it would be doable.

(PIE) Given sets

A_1,A_2,\dots,A_n

\lvert\bigcup_{i=1}^n A_i\rvert=\sum_{S\subseteq \{1,2,\ldots n\}} (-1)^{\lvert S\rvert+1}\lvert\bigcap_{i\in S} A_i\rvert

The point of PIE is to count each element once, and to prove that some element

X

is counted exactly once, pair every set without

X

with the exact same set but with

X

included. The values of these will cancel out and you will be left with only

\{X\}

, which contributes

1

to the sum.

My point is, if you are not taking notes, you are refusing to see these connections. Part of math is “seeing the big picture”, but if you don’t have a ton of related problems together, how are you supposed to see this big picture? So to reiterate, take notes!