Common Sudoku Variants

Puzzle shown: Classic Sudoku by Cracking the Cryptic

There are 9 rows, 9 columns, and 9 $3\times 3$ regions. Each square must be filled with a digit from $1$ to $9$, and digits may not repeat in the same row/column/region.

In almost every sudoku puzzle, these rules will apply.

Local Constraints

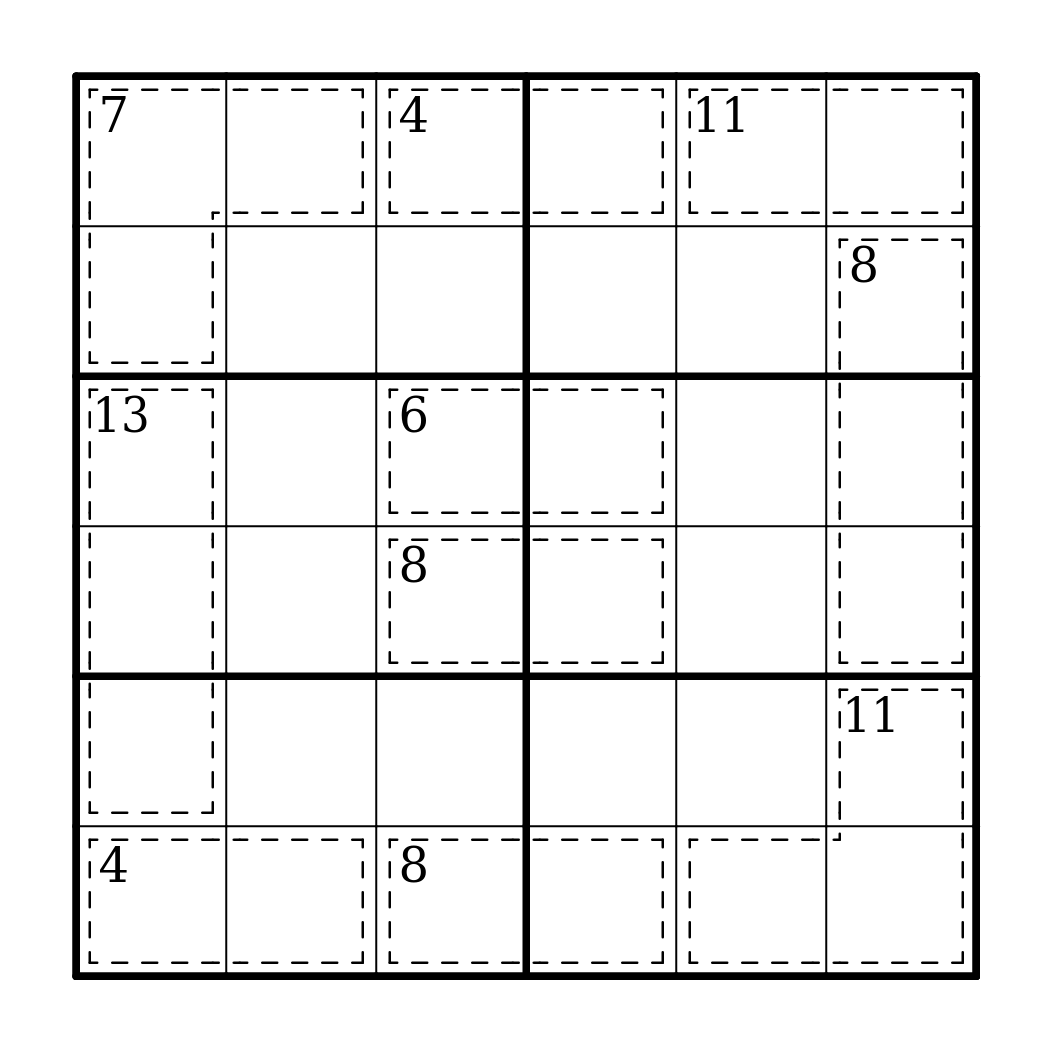
Killer Cages

Puzzle shown: Killer Sudoku by Serkan Yürekli

Orthogonally connected cages are drawn. No digits in the same cage may repeat, and if a sum is indicated in the cage, the digits in the cage add up to said sum.

Thermo

Digits must be strictly increasing from the bulb of the thermometer to the end.

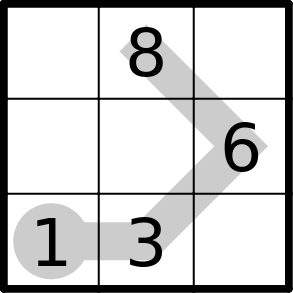
Arrows

Digits on the arrow must add to the digit in the circle. Digits may repeat if permitted by other Sudoku rules.

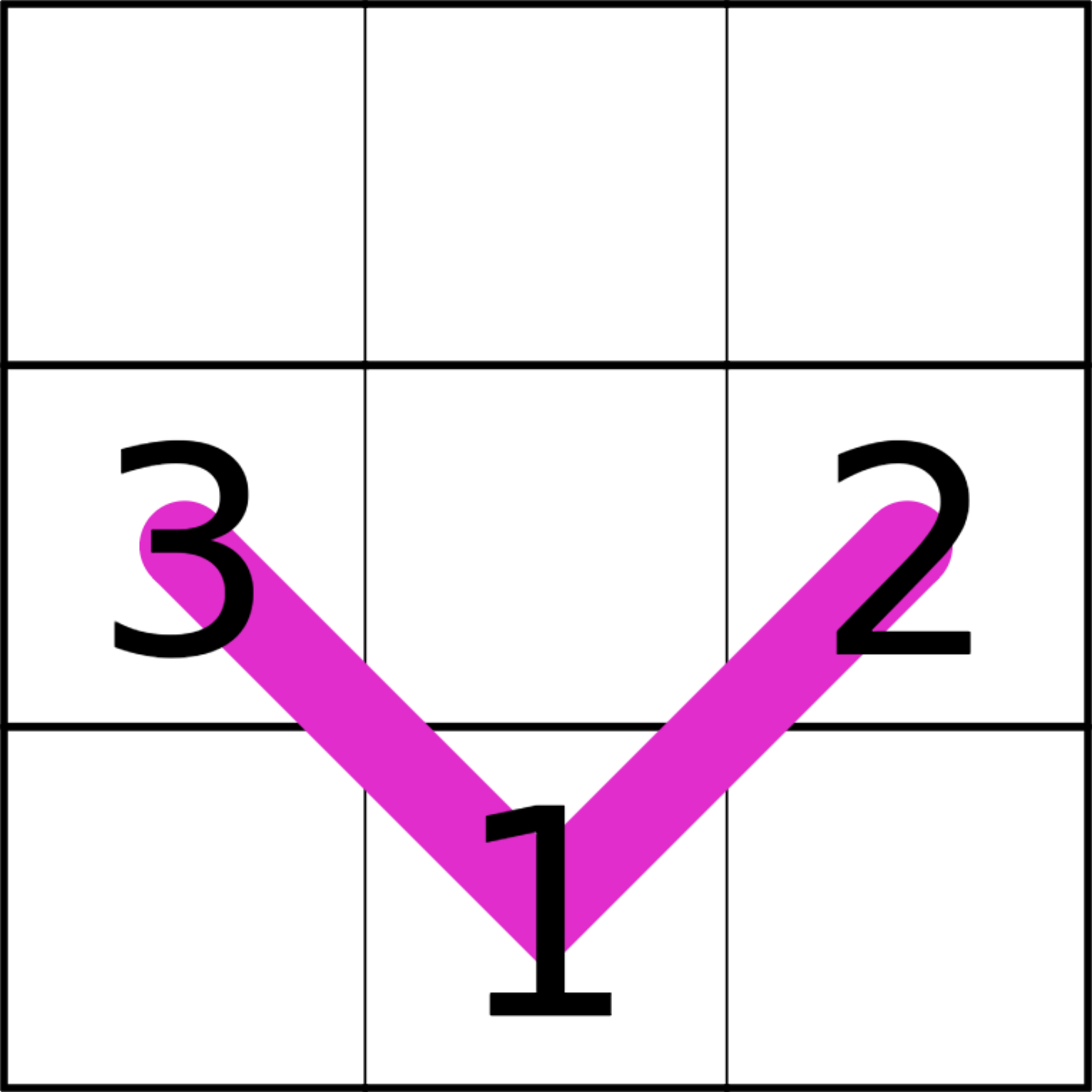
Renban Lines

Renban lines must contain consecutive digits in any order.

German Whispers

Two directly connected digits on a German whisper must differ by 5 or more.

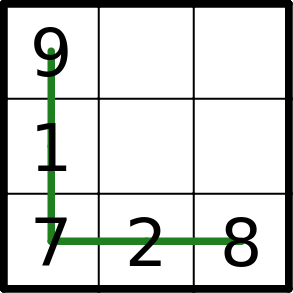
X/V

Two digits separated by an X must sum to 10. Two digits separated by a V must sum to 5. (These digits are orthogonally adjacent.)

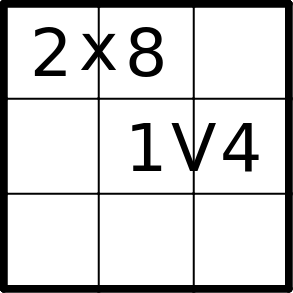
Kropki

If two orthogonal digits are separated by a white dot, they must be consecutive. If two orthogonal digits are separated by a black dot, one must be double the other.

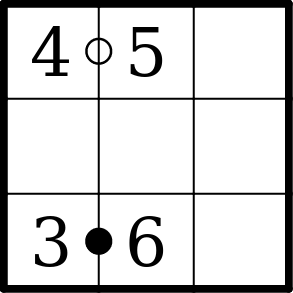
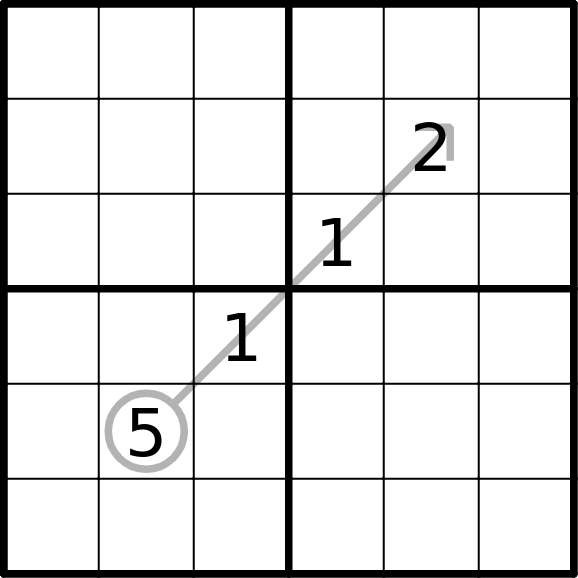
Little Killers

The digits on the diagonal indicated by a Little Killer must add to the sum indicated by the Little Killer. Digits on the diagonal may repeat.

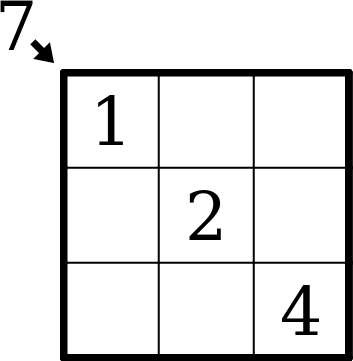
X-Sums

The first X digits in a row or column in the direction of an X-Sum, where X is the first digit seen in that row or column, must add to the indicated sum.

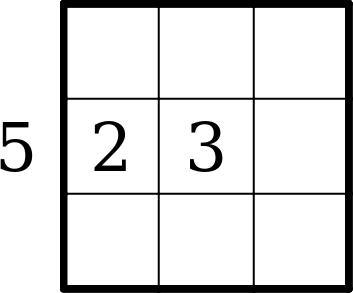
Odd/Even

Gray circles must contain odd digits, and gray squares must contain even digits.

Between Lines

Digits on a between line must lie between the digits on the endpoints. Digits may repeat on the line.

Global Constraints

Anti-knight

A square must contain a digit different from every other square a knight’s move away (2 over and 1 across).

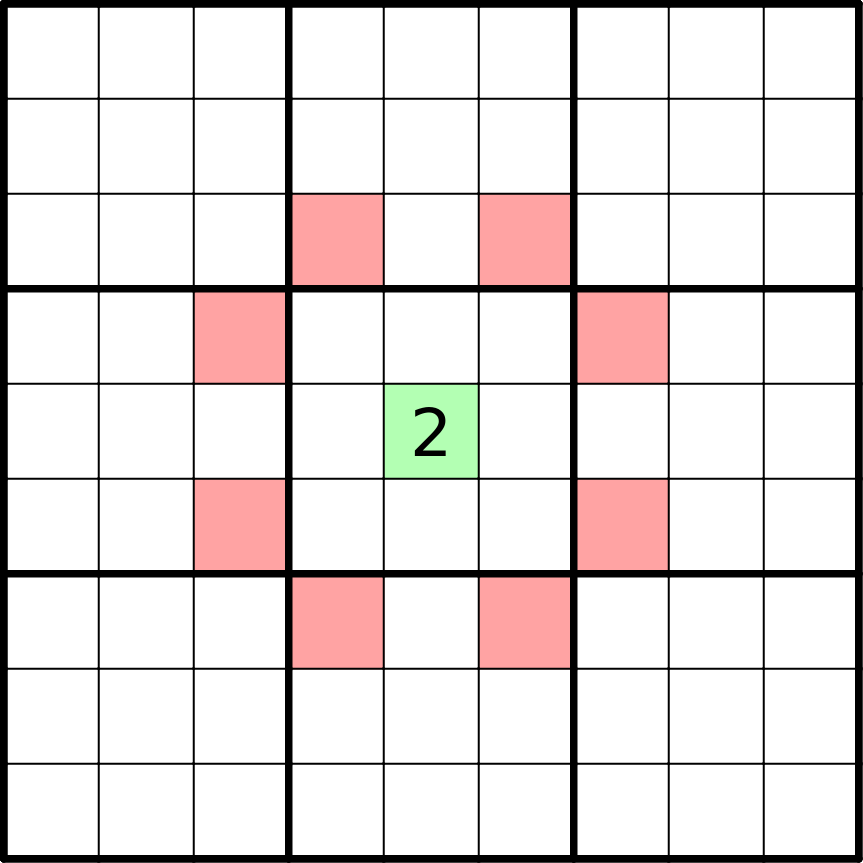
Anti-king

A square must contain a digit different from every other square a king’s move away (sharing a vertex).